Free Gmat Practice Test For Mac

Posted on  by 



Our GMAT Practice Test and Study Guide PDF contains Real Questions and Answers. You can download 100% free PDF to try before you register for Premium Files. To ace this exam, all you have to do is download GMAT Dumps File, memorize the Questions and Answers, Practice with our VCE Exam Simulator and you are ready for Real Test. Realistic Practice. Experience the GMAT ® before test day with a realistic practice test. See how you'd score, and get a detailed report of your strengths and weaknesses. You'll also get two weeks of access to instructional videos and additional practice covering some of the most important topics on the GMAT.

Nokia x3-02 usb drivers free download Download Nokia X3-02 USB AT smartphone drivers or install DriverPack Solution software for driver update. Download Download DriverPack Online. Nokia X3-02 USB AT smartphone drivers. Install drivers automatically. DriverPack software is absolutely free of charge. Available drivers (1).

STEP #2: Download kmsauto lite from here. STEP#3: After you have downloaded install the software. STEP #4: Launch the installed file and click on the activate windows and office. You are done with activating your windows. I'll let you know how you can use this app, but first, let's have a recap to some of the features of kmsauto. DOWNLOAD KMSauto All you need is to download the activator from button above. Unzip the activator by using the password windows. After the extraction, run the file KMSAuto Net. Windows It is the so-called «Lightweight» version of the standard CMS engine based activator. It differs from the full version. All basic settings are hidden from users ‘ eyes. So nobody can do harm by clicking on everything. The activator can work with Windows 7 (all editions), Windows 8, 8.1, and Windows. What is KMSAuto Lite. KMSAuto Lite 1.5.6 is automatic and 100% working KMS activator for Microsoft Windows 10, Windows Server 2019 series and Microsoft Office 2020. It’s a secure and fully automatic KMSAuto activator for Windows Vista, 7, 8, 8.1, 10, Windows Server 2008, 2012, 2016, 2019 series operating systems, and Microsoft Office 2010, 2013, 2016, 2019.

The GMAT Problem Solving questions will test your ability to evaluate information and solve numerical problems. Our practice problems are designed to be very challenging in order to prepare you for the harder-level questions found on the GMAT. Answers and detailed explanations are include with each problem. Start your test prep now with our free GMAT Problem Solving practice test.

Is Toad for Oracle available for Mac? 261424, Toad for Oracle is not available for Mac, as alternative a virtual machine can be created in the Mac OS, and install Microsoft Windows and then install Toad for Oracle.Right now only Toad Edge supports Mac OS, Toad Edge can work with MySQL. Toad for oracle para mac. Toad is an macOS database development and management application for Oracle, PostgreSQL, MySQL and MongoDB. It allows you to work with all of these platforms easily, as it features an intuitive. Toad is a free Mac program, that belongs to the category Development. Toad® for Oracle - Sensitive Data Protection Find and control sensitive data across all your Oracle databases Quickly discover sensitive data across all your Oracle databases for GDPR compliance and other regulations Automates discovery, streamlines reporting and automatically notifies developers when they’re referencing sensitive data.

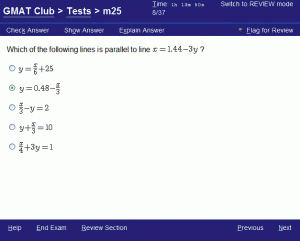
Directions: Solve the problem and select the best of the answer choices given.

Please wait while the activity loads.
If this activity does not load, try refreshing your browser. Also, this page requires javascript. Please visit using a browser with javascript enabled.
If loading fails, click here to try again
Congratulations - you have completed . You scored %%SCORE%% out of %%TOTAL%%. Your performance has been rated as %%RATING%%
The City Opera House is expanding. Currently the city block containing the opera house is rectangular-shaped with a total volume of 9600 feet. If the expanded Opera House is 2.5 times as long, wide, and deep as the original building, what would the new volume be?
60,000
150,000
The correct response is (D). The volume is the length x width x height. The building’s original volume is equal to lwh = 9600. The new footage will be 2.5l x 2.5w x 2.5h, or (lwh) x 2.5 x 2.5 x 2.5 = 15.625(lwh). Since lwh = 9600, the new volume will be 15.625(9600) = 150,000.
In a university club of 200 people, the number of Political Science majors is 50 less than 4 times the number of International Relations majors. If one fifth of the club members are neither Political Science majors nor International Relations majors, and no club member is majoring in both Political Science and International Relations, how many of the club members are International Relations majors?
50
95
The correct response is (A). Let P be the number of Political Science majors and let R be the number of International Relations majors. 'One fifth of the legislators are neither,' so there are 1/5 *200 = 40 legislators who are neither. Hence, there are 200 – 40 = 160 Poly-Sci majors and IR majors, or P + R = 160. Translating the clause 'the number of Poly-Sci majors is 50 less than 4 times the number of IR majors' into an equation yields P = 4R – 50.
Plugging this into the equation P + R = 160 yields:
4R – 50 + R = 160
5R – 50 = 160
5R = 210
R = 42
If the total cost of 20 pairs of shoes is equal to the total revenue generated from the sale of 25 pairs of shoes, what is the percent of profit or loss made on the sale of each pair of shoes, assuming each pair of shoes cost the same dollar amount and each pair of shoes sold for the same dollar amount?
25% profit
20% profit
The correct response is (C). The need-to-know formula here is: Profit/Loss % = (Sales Price – Cost Price) / Cost Price x 100. The stem tells us that 20c = 25s, or 4c = 5s, so the ratio of the sales price to the cost price is 4/5.
Let’s simplify our Profit/Loss % formula by dividing each term by the cost price: Profit/Loss % = (S/C – C/C) x 100
P/L% = (S/C – 1) x 100 We know that S/C = 4/5 for this problem. So we can plug in and solve:
P/L% = (4/5 – 1) x 100
P/L% = (-1/5) x 100
P/L% = -20%. The answer is a 20% loss.
Clarissa spent all day on a sightseeing trip in Britain. Starting from her hotel, Clarissa boarded a bus, which traveled at an average speed of 15 miles per hour through a 30 mile section of the countryside. The bus then stopped for lunch in London before continuing on a 3 hour tour of the city's sights at a speed of 10mph. Finally, the bus left the city and drove 40 miles straight back to the hotel. Clarissa arrived at her hotel exactly 2 hours after leaving London. What was the bus's average rate, approximately, for the entire journey?
14
25
The correct response is (B). To find the 'Average Rate' of the bus, we know we will need to find the Total Distance and the Total Time, so let's see how we can use the D = R x T formula to find the missing info.
For the first part of the trip, we know that 30 miles = 15mph x T, so we know that T = 2 hours. For the middle part of the trip, we know that D = 10mph x 3 hours, so we know that D = 30 miles. For the last part of the trip, we know that 40 miles = R x 2 hours, so we know that R = 20mph.
Now we can find the Total Distance and the Total Time. Total Distance = 30 miles + 30 miles + 40miles = 100 miles. Total Time = 2 hours + 3 hours + 2 hours = 7 hours. So the Average Rate = 100 miles/ 7 hours = 14.28mph. (B) is the closest approximation.
Meredith jogged to the top of a steep hill at an average pace of 6 miles per hour. She took the same trail back down. To her relief, the descent was much faster; her average speed rose to 14 miles per hour. If the entire run took Meredith exactly one hour to complete and she did not make any stops, how many miles, approximately, is the trail one way?
3
5
The correct response is (C).
Time = Distance/Rate
Time spent going uphill = D /6
Time spent going downhill = D/14
Total Time = 1 hour
We can write the following equation, and solve for D:
Time taken on the uphill journey + Time taken on the downhill journey = Total Time

Gmat Online Test Free

At a medical research lab, nine doctors are conducting multiple clinical trials. Six of the doctors are working on a clinical trial with exactly one other doctor and three doctors are working on a clinical trial with exactly two other doctors. If two doctors are selected at random from the lab, what is the probability that those two doctors are NOT working together on a clinical trial?
2/12
7/12
The correct response is (E). Remember that the probability of something NOT occurring is 1 – the probability of it occurring. So for this question, we can find the probability that those two doctors WILL be working together, then subtract it from one. Let’s start with the first group. If the first person we chose was from the first group, the odds that the second person would be their partner would be 1/8. This is because every doctor in the first group only has ONE partner, and we’d have 8 people to choose from after picking the first person (out of 9 total). 6/9*1/8 = 6/72 = 1/12.
If the first person we chose was from the second group (probability = 3/9), the odds that the second person would be one of their partners would be 2/8. The numerator is 2 this time because each person in the second group has two partners instead of one. 3/9*2/8 = 6/72 = 1/12.
Since EITHER of these outcomes (picking the first person from the first group OR the second group) produces our desired result, we’ll add these probabilities. 1/12 + 1/12 = 2/12 = 1/6.
Therefore, the probability that the two doctors are NOT working together is 1 – 1/6 = 5/6.
Another way to think of this question is to assign letters to each doctor and group them by clinical trial. So AB, CD, EF are from the first group, and GHI are from the second group. There are 6 ways of choosing a pair that are working together: AB, CD, EF, GH, GI, or HI. And we can quickly use the combination formula to find the total possible ways to choose 2 from 9. 9C2 = 9! / 2! 7! = 9 x 8/2 = 72/2 = 36. 6/36 = 1/6.
Free Gmat Practice Test For MacGmat
For which of the following functions g is g(z) = g(1 – z) for all z?
g(z) = 1 – z2
g(z) = z2(1 – z)2
The correct response is (D). For questions with functions in the answer choices, use the given definitions to check each of the answer choices. For instance, since we want f(z) = f(1-z) we can assume z=4, and check each of the answer choices to see if f(4) = f(1-4), or, f(4) = f(-3).
If you notice that, then it very easy to find the solution, replace each function with 4 and -3 instead of z, and see if f(4)=f(-3).
Let’s try choice (A):
F(-3) = 1 – (-3) = 4
F(4) = 1 - (4) = -3
They are NOT equal. Eliminate.
Repeat this process for the other answer choices, until you find one for which f(4) = f(-3). That choice is D:
F(-3) = (-3)2 (1 – (-3))2 = (9)(16)
F(4) = (4)2 (1 – (4))2 = (16)(9)
F(-3) = F(4).
A right triangle has sides that are consecutive even integers. The longest side is z. Which of the following equations could be used to find z?
(z – 2)2 = (z – 4) – z2
(z – 2)2 = z2 – (z - 1)2
Free gmat practice test for macbook pro

Free Gmat Practice Test Pdf

The correct response is (A). If we know the longest side is “z,” we can label the other two sides as “z-4” and “z-2” respectively because we know that “consecutive even” means each side differs from its next-largest neighbor by 2. For example: 6, 8, 10.
We would use the Pythagorean Theorem to find the value of z:
a2 + b2 = c2
(z – 2)2 + (z – 4)2 = z2
Remember that “c” is always the hypotenuse, or the longest side. Only choice (A) matches this equation.
Rectangle LMNO is inscribed in a circle with center P. If the area of the rectangle is 8 times its width, and the distance from P to side LM is 3, what is the circle’s approximate circumference?
10
45
The correct response is (C). To find the circumference of a circle, we must find the radius. Let’s start with what we know:
The area of a rectangle is lw. Here we are told that lw = 8w. That means the length is 8. We also know that the distance from P to LM = 3, so the length of the rectangle must be 6. Let’s re-draw the shape:
The radius of the circle, LP, is the hypotenuse of a right triangle whose other two sides are half the length and half the width of the rectangle. Since it’s a classic Pythagorean triplet (3:4:5), we don’t need to use the Pythagorean theorem.
Plug the radius into the formula for circumference: C = 2πr. C = 2*π*5. The circumference is approximately 10π, or a number slightly larger than 30.
Larry’s Lawn Service charges $w/hour for the first x hours of grass trimming, then w + 2 dollars for every hour of work over x hours. How much more will a homeowner be charged for a grass trimming job that took z hours if z > x than for a job which took only w hours if x < w < z?
(w + 2) – zx
xw + 2 – (z – w)
The correct response is (C). We can solve this problem by picking numbers:
We want x < w < z. Let’s pick x=3, w=4, z=6
For a job that took 4 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last hour. The total cost would be $4(3) + $6(1) = $12 + $6 = $18.
For a job that took 6 hours, the client is charged $4/hour for the first 3 hours, then $6/hour for the last three hours. The total cost would be $4(3) + $6(3) = $12 + $18 = $30. The difference in price is $12.
Let’s plug our values into the expression: (w+2)(z-w) = (4+2)(6-4) = 6*2 = 12.
Here is the algebraic solution:
If the grass trimming job took z hours, the total cost is: wx + (z-x)(w+2)
If the grass trimming job took w hours, where x < w < z, the total cost is: wx + (w-x)(w+2)
The extra cost will be:
[wx + (z-x)(w+2)] – [wx + (w-x)(w+2)]
= (z-x)(w+2) - (w-x)(w+2)
= (w+2)[(z-x) – (w-x)]
= (w+2)(z-w)

Free Gmat Practice Exams

Once you are finished, click the button below. Any items you have not completed will be marked incorrect.
12345
678910
End

Next Practice Test:
Problem Solving Practice Test 2>>

Free Gmat Practice Test Online

More Practice Tests:
More Quantitative Tests>>
Integrated Reasoning Tests>>
Verbal Tests>>
Main Menu>>





Coments are closed
What Is A Dreadnought Acoustic Guitar How To Set Up Iphone Emulator On Mac Air